Voir aussi : Angles de deux vecteurs, Les transformations
Problème
Considérons deux vecteurs non nuls  et leur image
et leur image  par une transformation.
par une transformation.
Il s'agit de comparer les angles orientés
 et
et  .
.
On étudiera le cas d'une translation,
d'une symétrie axiale, d'une homothétie,
d'une rotation.
Cliquer sur les différentes figures pour les activer.
|
Par la translation de vecteur On a : En effet, pour une translation on a Voir aussi : les translations |
|
|
Par la symétrie d'axe (EF) les
vecteurs "bleus" On a :
Cet exemple illustre le fait qu'une symétrie axiale transforme un angle orienté en son opposé. Voir aussi : les symétries axiales |
|
|
Par l'homothétie de centre I et de rapport
-1,5 les vecteurs "bleus" On a : Cet exemple illustre le fait qu'une homothétie conserve les angles orientés. On peut modifier le rapport de l'homothétie à l'aide des touches "flèche haut" et "flèche bas". Voir aussi : les homothéties |
|
|
Par la rotation de centre I et d'angle 60°
les vecteurs "bleus" On a : Cet exemple illustre le fait qu'une rotation conserve les angles orientés. On peut modifier l'angle de la rotation à l'aide des touches "flèche haut" et "flèche bas" Voir aussi : les rotations |
 les vecteurs "bleus"
les vecteurs "bleus"  ont pour images les vecteurs "rouges"
ont pour images les vecteurs "rouges"  .
. .
. .
. ont pour images les vecteurs "rouges"
ont pour images les vecteurs "rouges"  .
. .
. ont pour images les vecteurs "rouges"
ont pour images les vecteurs "rouges"  .
.  .
. ont pour images les vecteurs "rouges"
ont pour images les vecteurs "rouges" 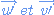 .
. .
.