Les rotations du plan
Les rotations sont des transformations
Définition
La rotation r de centre O et d'angle  permet d'associer à chaque
point M du plan le point M' unique du plan défini par :
permet d'associer à chaque
point M du plan le point M' unique du plan défini par :
Si M=O alors M'=M
Sinon M' est le point défini
par:  et OM=OM'
et OM=OM'
Le point M'
est appelé image de M par la rotation r. On peut noter
M' =r(M).
Théorème des points invariants
Si 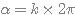 alors tout point est invariant
alors tout point est invariant
Sinon O est le seul point invariant
|
Pour construire l'image d'un point A par
la rotation de centre O et d'angle par exemple,  (c'est à dire 60°): (c'est à dire 60°):
|
|

Théorème: conservation des distances
Les
rotations conservent
les distances : quels que soient les points A et B d'images A' et B' , A'B'=AB
Les rotations sont donc
des isométries
|
|
|

Théorème: conservation des angles
Les rotations conservent
les angles : quels que soient les points A, B et C d'images A', B' et C' ,  =
=
|
|
|

Théorème: conservation de l'alignement
Les
rotations
conservent l'alignement: si trois points A, B et C sont alignés alors
leurs images A', B' et C' sont alignées.
|
|
|

Modification
de l'angle de la rotation
|
L'angle en radians
de cette rotation est l'angle orienté  . .
On peut modifier cet angle en modifiant la position de I' sur le cercle.
|
|

 permet d'associer à chaque
point M du plan le point M' unique du plan défini par :
permet d'associer à chaque
point M du plan le point M' unique du plan défini par : et OM=OM'
et OM=OM'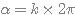 alors tout point est invariant
alors tout point est invariant (c'est à dire 60°):
(c'est à dire 60°): =
=
 .
.