Soit f une fonction continue sur un intervalle [a;b].
Si f est positive sur [a;b] alors
est positive.Quelques propriétés de l'intégrale
Voir également : Valeur moyenne ; Intégrales (val numériques) ; Intégrales (Opération sur les fonctions intégrées)
Intégrale d'une fonction périodique ; Intégrales numériques
Positivité
Théorème
Soit f une fonction continue sur
un intervalle [a;b].
Si f est positive sur [a;b] alors
est positive.
Faire varier les valeurs a et b
et vérifier que lorsque f est positive sur [a;b], son intégrale sur cet intervalle
l'est aussi.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel
La réciproque est fausse.
L'intégrale d'une fonction sur
un intervalle [a;b] peut être positive sans que cette fonction ne
soit positive
sur cet intervalle.
Trouver des valeurs de a et b
telles que l'intégrale de f soit positive sur [a;b] sans que f
ne le soit sur ce même intervalle.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel
Relation de CHASLES
Relation de CHASLES
Soit f une fonction continue
un intervalle I. Pour tous réels a, b et c de cet intervalle :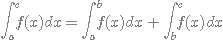 
.
Faire varier les valeurs a,
b et c et observer les valeurs respectives des intégrales.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel
Comparaison
Théorème
Soient f et g deux fonctions continues sur
un intervalle [a;b].
Si f 
g sur [a;b] alors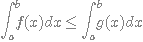 
.
Faire varier les valeurs a,
b et c et observer les valeurs respectives des intégrales.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel
La réciproque est fausse
Si, sur un même intervalle [a;b],
l'intégrale d'une fonction g est supérieure à l'intégrale d'une fonction
f, alors g n'est pas forcément supérieure à f sur cet intervalle.
Trouver des valeurs de a et b
telles que l'intégrale de g soit supérieure à celle de f sans pour autant que
g soit supérieure à f sur cet intervalle.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel
Encadrement d'une intégrale
Théorème
Soit f une fonction continue sur un intervalle
I et soient a et b deux réels de cet intervalle.
Si m et M
sont deux réels tels que m 
f 
M sur [a;b], alors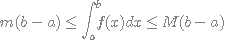 
Faire varier les valeurs a,
b, m et M et observer les valeurs respectives des intégrales.
En enfonçant la touche Ctrl et en déplaçant la souris,
vous pouvez déplacer la zone représentée.
Un clic droit donne accès au menu
contextuel