On appelle plan complexe, le plan muni d'un repère orthonormé direct (O,
,
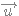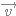). A tout complexe de la forme a+ ib on associe, dans le plan
complexe, le point de coordonnées (a;b), appelé
image de z.Ecritures d'un nombre complexe
Définition 1
On appelle nombre complexe tout
nombre pouvant s'écrire sous la forme a+ ib où
a et b sont réels et où i vérifie la propriété
i² = -1.
a + ib est l'écriture
algébrique du nombre complexe z.
a est la partie
réelle de z et b sa partie imaginaire.
Interprétation géométrique
On
appelle plan complexe, le plan muni d'un repère orthonormé direct (O,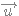,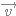). A tout complexe de la forme a+ ib on associe, dans le plan
complexe, le point de coordonnées (a;b), appelé
image de z.
Définition 2
L'argument de z est noté
et le module de z est noté 
.
z peut s'écrire : 
, cette écriture est l'écriture trigonométrique de
z.
Définition 3
Le nombre complexe peut aussi être écrit 
, c'est l'écriture exponentielle de z.
Déplacer z et
observer ses différentes écritures
