Généralités
Définition 1
On appelle fonction trinôme, à coefficients réels, toute fonction,
définie sur R, qui à x associe une expression pouvant s'écrire
sous la forme ax²+bx+c
où a, b et c sont des réels avec a non nul.
Dans la figure, modifier a, b et c à la souris.
Résolution dans R
Définition
2
On appelle racine du trinôme ax²+bx+c, toute valeur de x annulant le trinôme.
Définition 3
Soit ax²+bx+c
un trinôme du second degré en x à coefficients réels. On appelle discriminant de
ce trinôme le réel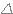 
= b²-4ac
Théorème 1
Soit ax²+bx+c un
trinôme du second degré en x réel à coefficients réels a, b et c avec
a non nul.
* Si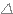 
> 0 alors le trinôme admet 2 racines réelles distinctes.
* Si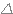 
= 0, alors le trinôme admet une unique racine réelle.
* Si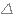 
< 0, le trinôme n'admet aucune racine réelle.
Dans la figure, modifier a, b et c à
la souris et observer le nombre de solutions réelles en fonction de la valeur
du discriminant.
On peut également étudier le signe de ce trinôme
Résolution dans C
Théorème 2
Soit az²+bz+c un
trinôme du second degré en z complexe à coefficients réels a, b et c avec
a non nul.
* Si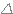 
> 0 alors le trinôme admet 2 racines réelles distinctes.
* Si 
= 0, alors le trinôme admet une unique racine réelle.
* Si 
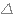< 0, le trinôme admet deux racines complexes non réelles conjuguées
distinctes.