Théorème des valeurs intermédiaires
Théorème
Soit 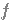 une fonction définie sur un intervalle I et
une fonction définie sur un intervalle I et 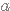 et
et
 des réels de I.
des réels de I.
Si 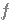 est continue
alors pour tout réel
est continue
alors pour tout réel 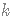 compris entre
compris entre 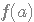 et
et 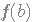 , il existe au
moins un réel
, il existe au
moins un réel 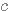 ,
compris entre
,
compris entre 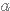 et
et
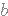 tel que
tel que 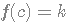 .
.
Attention, la réciproque
est fausse !
Le réel " "
peut ne pas être unique !
"
peut ne pas être unique !
Cliquer sur la figure afin de la rendre
active
Faire varier à l'aide des touches de direction, la valeur
de k entre f(a) et f(b).
"n" indique le nombre de solutions de l'équation f(x)
= k

Que
se passe t-il si 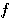 n'est pas continue ?
n'est pas continue ?
Cliquer sur la figure afin de la rendre
active
Faire varier à l'aide des touches de direction, la valeur
de k entre f(a) et f(b).
"n" indique le nombre de solutions de l'équation f(x)
= k
|

La réciproque
est fausse : l'existence du réel "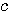 "
n'entraîne pas la continuité de "
n'entraîne pas la continuité de 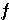 : :
Cliquer sur la figure afin de la rendre
active
Faire varier à l'aide des touches de direction, la valeur
de k entre f(a) et f(b).
L'équation f(x)
= k peut
admettre des solutions bien que f ne soit pas continue.
"n" indique le nombre de solutions de l'équation f(x)
= k
|

|
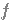 une fonction définie sur un intervalle I et
une fonction définie sur un intervalle I et 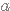 et
et
 des réels de I.
des réels de I. 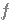 est continue
alors pour tout réel
est continue
alors pour tout réel 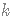 compris entre
compris entre 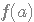 et
et 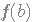 , il existe au
moins un réel
, il existe au
moins un réel 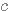 ,
compris entre
,
compris entre 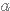 et
et
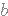 tel que
tel que 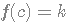 .
. "
peut ne pas être unique !
"
peut ne pas être unique !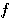 n'est pas continue ?
n'est pas continue ? "
n'entraîne pas la continuité de
"
n'entraîne pas la continuité de 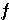 :
: