Dx est la différence x2 - x1, Dy est la différence y2 - y1 et R est le rapport de ces accroissements,
ici
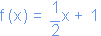.Définition
Une fonction f est dite affine si elle est définie sur R par
f(x) = ax + b, où a et b sont des nombres réels.
Théorème
Soit une fonction f définie sur R , si f est une fonction affine alors les accroissements de x et f(x)
sont proportionnels.
Réciproquement si les accroissements de x et f(x)
sont proportionnels alors f est une fonction affine, le coefficient de proportionnalité est égal
à a.
Voir un contre-exemple, voir l'exemple 1, voir
l'exemple 2
Exemple
1
Dx est la différence x2
- x1, Dy est la différence y2
- y1 et R
est le rapport de ces accroissements,
ici .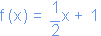
Cliquer sur la figure afin de la rendre active.
On peut modifier les valeurs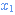 
ou 
à la souris.
Exemple 2
Dx est la différence x2
- x1, Dy est la différence y2
- y1 et R
est le rapport de ces accroissements,
ici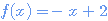 
.
Cliquer sur la figure afin de la rendre active.
On peut modifier les valeurs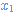 
ou 
à la souris.
Contre-exemple: la fonction carré
Ax est la différence x2 - x1, Ay est la différence y2 - y1 et R est le rapport de ces accroissements, ici R varie.
Cliquer sur la figure afin de la rendre active
On peut modifier les valeurs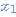 
ou 
en cliquant dessus et maintenant le doigt appuyé.