Soit
et 
deux vecteurs non nuls,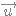 
et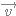 
sont colinéaires si et seulement si 
et 
ont la même direction.Définition
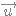Soit et deux vecteurs non nuls, et 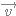sont colinéaires si et seulement si et ont la même direction.
Propriété 1
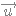et 
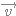sont colinéaires si et seulement si il existe un réel k
non nul tel que 
.
Remarque
Pour 
on a 
, par extension, on dit que le vecteur nul est colinéaire à
tout vecteur du plan.
Propriété 2
Deux vecteurs sont colinéaires si et seulement si leurs coordonnées
sont proportionnelles.
Cliquer sur la fenêtre pour la rendre active.
Les vecteurs 
et 
sont colinéaires, avec 
, faire varier k à l'aide des flèches de direction.
