Soit f une densité de probabilité. Une variable aléatoire X est associée à la densité f si pour tout réel X : p(X<x) =
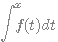
Voir également : Schéma de Bernouilli - Loi de Bernouilli - Loi binomiale - Loi de probabilité
Définition 1
On appelle densité de probabilité toute fonction définie sur un intervalle I, continue, positive et dont l'intégrale sur I est égale à 1.
Définition 2
Soit f une densité de probabilité. Une variable aléatoire X est associée à la densité f si pour tout réel X : p(X<x) =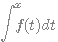
Remarque
Dans ce cas, pour tout x, p(X=x)=0
Théorème
Soit f une densité de probabilité et X une variable aléatoire associée à la densité f . Alors p(c<X<d) =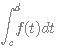 
Illustration : la loi normale ou loi de Laplace-Gauss
Définition
Une variable aléatoire X suit une loi de probabilité uniforme sur un intervalle [a;b] si elle est associée à une densité de probabilité égale à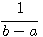 
sur l'intervalle [a;b].
Illustration
Loi exponentielle
Définition
Une variable aléatoire X suit une loi de probabilité exponentielle (appelée également loi de durée de vie sans vieillissement) de paramètre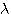 
>0 si elle est associée à la densité 
définie sur R+.
Illustration
Théorème
Soit X une variable aléatoire associée à une densité de probabilité exponentielle de paramètre 
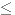>0. Alors pour tout réel positif x, P(X 
x) =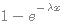 
.